En álgebra, la factorización es expresar un objeto o número (por ejemplo, un número compuesto, una matriz o un polinomio) como producto de otros objetos más pequeños (factores), (en el caso de números debemos utilizar los números primos) que, al multiplicarlos todos, resulta el objeto original. Por ejemplo, el número 15 se factoriza en números primos 3 × 5; y a²-b² se factoriza como binomio conjugados (a - b)(a + b).
de esta forma podras ejecutarlo:
martes, 14 de septiembre de 2010
martes, 7 de septiembre de 2010
Problema
.Si jesus dijo : debemos perdonar a nuestro projimo setenta veces siete .
plantea la ecuacion....
plantea la ecuacion....
TALLER N° 1
INTRODUCCIÓN A LA LÓGICA MATEMÁTICA POR MEDIO DE LOS BLOQUES LÓGICOS
Por: Clara Mejía L
PRESENTACIÓN :
Esta estrategia para la introducción de la lógica toma la vía experimental, en ella se acogen las propuestas de Z. P. Dienes y E. W. Golding, presentadas en el texto "Lógica y juegos lógicos" y se hacen las adaptaciones necesarias para la construcción de la lógica en los últimos grados de la secundaria.
El material desarrollado por Dienes se conoce como "bloques lógicos", nombre un tanto equívoco ya que pudiera pensarse que la lógica está en los bloques y no en las operaciones efectuadas entre los subconjuntos construidos con dichos bloques. En el desarrollo de la propuesta surgen de manera natural los conjuntos, los cuales constituyen un sustrato material donde se puede desarrollar la lógica.
5.2. CONDICIONES PEDAGÓGICAS
La utilización de los bloques lógicos, como mediadores para el establecimiento de los esquemas básicos del razonamiento lógico matemático, tiene las siguientes ventajas pedagógicas:
Proporciona un soporte material para la fijación de esquemas de razonamiento.
La forma en que los estudiantes realizan la actividad con ellos, constituye un indicador de las competencias necesarias para el desarrollo del pensamiento lógico. El maestro puede detectar, en el alumno, dificultades clasificatorias, que ya consideraba superadas.
El desarrollo del cálculo proposicional, a través de las actividades propuestas con este material, permite asimilar los contenidos proposicionales, eliminando las dificultades de tipo sicológico que se involucran, cuando se trabaja sobre enunciados del lenguaje ordinario.
Las operaciones lógicas se plasman en la formación de los conjuntos que verifican las propiedades expresadas por dichas operaciones. La lógica se va desarrollando a la par con la teoría de conjuntos.
5.3. OBJETIVOS
Construir, a partir del juego, esquemas básicos de razonamiento lógico.
Construir, tomando como primitivos, los conectivos lógicos "no" y "o", los restantes conectivos lógicos: "si... entonces", "y" y "si y sólo si".
Visualizar las propiedades más importantes de cada uno los conectivos y expresarlas en forma de leyes lógicas.
Mostrar en qué forma se niegan los conectivos, enunciando las leyes de De Morgan.
5.4. PRESENTACIÓN DE LOS BLOQUES LÓGICOS
Se trata de un conjunto de 48 piezas, diseñadas así:
Tres colores: amarillo, azul y rojo.
Cuatro formas: cuadrado, rectángulo, círculo, triángulo.
Dos tamaños: grande, pequeño.
Dos espesores: grueso, delgado.
Se tienen, entonces, cuatro variables, cuyos valores producen 48 figuras diferentes, el producto de 3 x 4 x 2 x 2.
El material debe ser libremente manejado por los jóvenes, antes de comenzar a plantear actividades. Es necesario que aprendan a nombrar cada uno de los bloques de acuerdo con sus cuatro características.
5.5. JUEGOS
5.5.1. Juego de la pieza escondida.
Un joven esconde una pieza. El resto del equipo tiene que descubrir cuál ha sido la pieza escondida. Inicialmente, se permite que los jóvenes manipulen los bloques y hagan sus ordenaciones. Más adelante, se les sugiere que descubran la pieza que falta sin tocar las demás.
Una variación, más complicada, podría ser esconder tres piezas escogidas, por ejemplo tres colores distintos, pero de la misma forma, del mismo tamaño y del mismo grosor.
5.5.2. Juego de negación con dos equipos.
Finalidad del juego: Si una cosa está en un determinado sitio, no puede estar al mismo tiempo en otra parte. (Principio de no contradicción).
Se forman dos equipos; se colocan a lado y lado de una mesa con una pantalla de separación, de modo que cada equipo pueda observar sus bloques únicamente. Cada equipo posee 24 bloques elegidos al azar. Se trata de que cada equipo debe pedir al otro los bloques que posee, designándolos con los cuatro atributos. Cuando un bloque ha sido pedido una vez, no puede volver a pedirse.
5.5.3. Juego de las respuestas y deducciones.
Para este juego, deben tenerse unas tarjetas con las siguientes inscripciones: no, grueso, delgado, grande, pequeño, cuadrado, rectángulo, círculo, triángulo, amarillo, azul y rojo.
Un joven piensa en un bloque y, seguidamente, sus compañeros le formulan preguntas como: ¿es grande? ¿es rojo?... A estas preguntas, el joven responde sí o no. Cada vez que se hace una pregunta, se coloca en la mesa la tarjeta donde está escrita la propiedad preguntada. Si la respuesta es negativa, se coloca la tarjeta con la palabra no, a la izquierda de la tarjeta correspondiente a la pregunta; si es afirmativa, basta dejar la tarjeta en su lugar. De esta manera, se va conformando una columna con las respuestas dadas por el joven. Se puede formar otra columna al frente de la de las respuestas, en esta se colocan las deducciones que los muchachos sacan de las respuestas.
5.5.4. Juegos de diferencia.
5.5.4.1. Juego con una diferencia: Entre dos bloques lógicos hay, por lo menos, una diferencia. El juego siguiente sirve para ayudar a los muchachos a tomar conciencia de estas diferencias y semejanzas.
Un alumno coloca una pieza cualquiera del conjunto encima de la mesa. El alumno siguiente elegirá una pieza que difiera de la primera solamente en un atributo. Esta diferencia tendrá que referirse al tamaño, al grosor, al color o a la forma. El siguiente elegirá una pieza que se diferencie de la segunda, igualmente, por un solo atributo. El ejercicio continuará de esta manera, hasta que todas o casi todas las piezas estén colocadas en una hilera.
5.5.4.2 Juego con dos diferencias: Consiste en jugar en un tablero con dos direcciones, de izquierda a derecha y de atrás hacia adelante. En la línea de izquierda a derecha se colocan los bloques contiguos que tengan una sola diferencia y en la línea atrás - adelante, los que tengan dos diferencias. Un problema interesante y difícil es llenar las esquinas.
Para llenar el espacio marcado con ? es necesario tener en cuenta una diferencia con respecto a B2 y dos con respecto a B1. En muchos casos, será imposible, con las fichas disponibles, llenar este lugar. Cuando esto ocurra, debe construirse una argumentación explicando el por qué de la imposibilidad.
5.5.4.3. Actividades. En los ejercicios que se presentan a continuación, coloque únicamente los bloques de acuerdo con las características anotadas en las cuadrículas respectivas. Determine el bloque o bloques que pueden ocupar la posición señalada con el signo "?".
Construya para cada situación una argumentación sistemática que le permita fundamentar la solución.
Por: Clara Mejía L
PRESENTACIÓN :
Esta estrategia para la introducción de la lógica toma la vía experimental, en ella se acogen las propuestas de Z. P. Dienes y E. W. Golding, presentadas en el texto "Lógica y juegos lógicos" y se hacen las adaptaciones necesarias para la construcción de la lógica en los últimos grados de la secundaria.
El material desarrollado por Dienes se conoce como "bloques lógicos", nombre un tanto equívoco ya que pudiera pensarse que la lógica está en los bloques y no en las operaciones efectuadas entre los subconjuntos construidos con dichos bloques. En el desarrollo de la propuesta surgen de manera natural los conjuntos, los cuales constituyen un sustrato material donde se puede desarrollar la lógica.
5.2. CONDICIONES PEDAGÓGICAS
La utilización de los bloques lógicos, como mediadores para el establecimiento de los esquemas básicos del razonamiento lógico matemático, tiene las siguientes ventajas pedagógicas:
Proporciona un soporte material para la fijación de esquemas de razonamiento.
La forma en que los estudiantes realizan la actividad con ellos, constituye un indicador de las competencias necesarias para el desarrollo del pensamiento lógico. El maestro puede detectar, en el alumno, dificultades clasificatorias, que ya consideraba superadas.
El desarrollo del cálculo proposicional, a través de las actividades propuestas con este material, permite asimilar los contenidos proposicionales, eliminando las dificultades de tipo sicológico que se involucran, cuando se trabaja sobre enunciados del lenguaje ordinario.
Las operaciones lógicas se plasman en la formación de los conjuntos que verifican las propiedades expresadas por dichas operaciones. La lógica se va desarrollando a la par con la teoría de conjuntos.
5.3. OBJETIVOS
Construir, a partir del juego, esquemas básicos de razonamiento lógico.
Construir, tomando como primitivos, los conectivos lógicos "no" y "o", los restantes conectivos lógicos: "si... entonces", "y" y "si y sólo si".
Visualizar las propiedades más importantes de cada uno los conectivos y expresarlas en forma de leyes lógicas.
Mostrar en qué forma se niegan los conectivos, enunciando las leyes de De Morgan.
5.4. PRESENTACIÓN DE LOS BLOQUES LÓGICOS
Se trata de un conjunto de 48 piezas, diseñadas así:
Tres colores: amarillo, azul y rojo.
Cuatro formas: cuadrado, rectángulo, círculo, triángulo.
Dos tamaños: grande, pequeño.
Dos espesores: grueso, delgado.
Se tienen, entonces, cuatro variables, cuyos valores producen 48 figuras diferentes, el producto de 3 x 4 x 2 x 2.
El material debe ser libremente manejado por los jóvenes, antes de comenzar a plantear actividades. Es necesario que aprendan a nombrar cada uno de los bloques de acuerdo con sus cuatro características.
5.5. JUEGOS
5.5.1. Juego de la pieza escondida.
Un joven esconde una pieza. El resto del equipo tiene que descubrir cuál ha sido la pieza escondida. Inicialmente, se permite que los jóvenes manipulen los bloques y hagan sus ordenaciones. Más adelante, se les sugiere que descubran la pieza que falta sin tocar las demás.
Una variación, más complicada, podría ser esconder tres piezas escogidas, por ejemplo tres colores distintos, pero de la misma forma, del mismo tamaño y del mismo grosor.
5.5.2. Juego de negación con dos equipos.
Finalidad del juego: Si una cosa está en un determinado sitio, no puede estar al mismo tiempo en otra parte. (Principio de no contradicción).
Se forman dos equipos; se colocan a lado y lado de una mesa con una pantalla de separación, de modo que cada equipo pueda observar sus bloques únicamente. Cada equipo posee 24 bloques elegidos al azar. Se trata de que cada equipo debe pedir al otro los bloques que posee, designándolos con los cuatro atributos. Cuando un bloque ha sido pedido una vez, no puede volver a pedirse.
5.5.3. Juego de las respuestas y deducciones.
Para este juego, deben tenerse unas tarjetas con las siguientes inscripciones: no, grueso, delgado, grande, pequeño, cuadrado, rectángulo, círculo, triángulo, amarillo, azul y rojo.
Un joven piensa en un bloque y, seguidamente, sus compañeros le formulan preguntas como: ¿es grande? ¿es rojo?... A estas preguntas, el joven responde sí o no. Cada vez que se hace una pregunta, se coloca en la mesa la tarjeta donde está escrita la propiedad preguntada. Si la respuesta es negativa, se coloca la tarjeta con la palabra no, a la izquierda de la tarjeta correspondiente a la pregunta; si es afirmativa, basta dejar la tarjeta en su lugar. De esta manera, se va conformando una columna con las respuestas dadas por el joven. Se puede formar otra columna al frente de la de las respuestas, en esta se colocan las deducciones que los muchachos sacan de las respuestas.
5.5.4. Juegos de diferencia.
5.5.4.1. Juego con una diferencia: Entre dos bloques lógicos hay, por lo menos, una diferencia. El juego siguiente sirve para ayudar a los muchachos a tomar conciencia de estas diferencias y semejanzas.
Un alumno coloca una pieza cualquiera del conjunto encima de la mesa. El alumno siguiente elegirá una pieza que difiera de la primera solamente en un atributo. Esta diferencia tendrá que referirse al tamaño, al grosor, al color o a la forma. El siguiente elegirá una pieza que se diferencie de la segunda, igualmente, por un solo atributo. El ejercicio continuará de esta manera, hasta que todas o casi todas las piezas estén colocadas en una hilera.
5.5.4.2 Juego con dos diferencias: Consiste en jugar en un tablero con dos direcciones, de izquierda a derecha y de atrás hacia adelante. En la línea de izquierda a derecha se colocan los bloques contiguos que tengan una sola diferencia y en la línea atrás - adelante, los que tengan dos diferencias. Un problema interesante y difícil es llenar las esquinas.
Para llenar el espacio marcado con ? es necesario tener en cuenta una diferencia con respecto a B2 y dos con respecto a B1. En muchos casos, será imposible, con las fichas disponibles, llenar este lugar. Cuando esto ocurra, debe construirse una argumentación explicando el por qué de la imposibilidad.
5.5.4.3. Actividades. En los ejercicios que se presentan a continuación, coloque únicamente los bloques de acuerdo con las características anotadas en las cuadrículas respectivas. Determine el bloque o bloques que pueden ocupar la posición señalada con el signo "?".
Construya para cada situación una argumentación sistemática que le permita fundamentar la solución.
Logica Matematica
La lógica matemática es una parte de la lógica y las matemáticas, que consiste en el estudio matemático de la lógica y en la aplicación de este estudio a otras áreas de las matemáticas. La lógica matemática guarda estrechas conexiones con la ciencias de la computación y la lógica filosófica.
La lógica matemática estudia los sistemas formales en relación con el modo en el que codifican conceptos intuitivos de objetos matemáticos como conjuntos, números, demostraciones y computación.
La lógica matemática suele dividirse en cuatro subcampos: teoría de modelos, teoría de la demostración, teoría de conjuntos y teoría de la recursión. La investigación en lógica matemática ha jugado un papel fundamental en el estudio de los fundamentos de las matemáticas.
La lógica matemática fue también llamada lógica simbólica. El primer término todavía se utiliza como sinónimo suyo, pero el segundo se refiere ahora a ciertos aspectos de la teoría de la demostración.
La lógica matemática no es la "lógica de las matemáticas" sino la "matemática de la lógica". Incluye aquellas partes de la lógica que pueden ser modeladas y estudiadas matemáticamente.
La lógica matemática estudia los sistemas formales en relación con el modo en el que codifican conceptos intuitivos de objetos matemáticos como conjuntos, números, demostraciones y computación.
La lógica matemática suele dividirse en cuatro subcampos: teoría de modelos, teoría de la demostración, teoría de conjuntos y teoría de la recursión. La investigación en lógica matemática ha jugado un papel fundamental en el estudio de los fundamentos de las matemáticas.
La lógica matemática fue también llamada lógica simbólica. El primer término todavía se utiliza como sinónimo suyo, pero el segundo se refiere ahora a ciertos aspectos de la teoría de la demostración.
La lógica matemática no es la "lógica de las matemáticas" sino la "matemática de la lógica". Incluye aquellas partes de la lógica que pueden ser modeladas y estudiadas matemáticamente.
lunes, 6 de septiembre de 2010
1. CAMPOS NUMÉRICOS.
En matemáticas básicamente se trabaja con números, la idea es aprender a identificar las diferentes clasificaciones en que podemos ubicar cada uno de los números que es llamado campos numéricos.
a. Números dígitos: Conjunto compuesto por los números con los cuales se forman los demás números. Por lo tanto los números dígitos están formados por los números 0,1,2,3,4,5,6,7,8 y 9. Asignémosle a estos números la letra D.
b. Números naturales: Conjunto formado por todos los enteros positivos. A estos números se les asigna la letra N. Son los números que utilizamos para contar.
c. Números enteros: Conjunto formado por los enteros positivos, enteros negativos y el cero. A estos números se les asigna la letra Z..
d. Números racionales: Un número racional es todo número que se pueda escribir como un cociente entre dos números enteros, con el denominador diferente de cero. Los matemáticos le asignaron la letra Q. De tal manera que los números racionales se definen matemáticamente.
e. Números irracionales: Un número irracional es todo número que no se puede escribir como un cociente entre dos números enteros. Podemos ver que un número no puede ser racional e irracional o sea si es racional no puede ser irracional, o la contrario, si es irracional no puede ser racional. A los irracionales los matemáticos le asignaron la letra H o la Q’. A los irracionales pertenecen las raíces no exactas y los decimales infinitos no periódicos.
Antes de continuar es necesario que aclaremos la clasificación de los números decimales que no forman un campo numérico sino que son más bien otra forma de escribir un número.
NÚMEROS DECIMALES: los números decimales pueden ser finitos e infinitos
Números decimales finitos: Son los decimales que tienen un número determinado de cifras decimales. Son ejemplo de ellos los siguientes. 0,25 que tiene dos cifras decimales (dos cifras después de la coma). 0,4528 con cuatro cifras decimales. 3256,2 con una cifra decimal.
Números decimales infinitos: estos números tienen un número indeterminado de cifras decimales, por esto todas las cifras no se pueden escribir y por ello se les colocan puntos suspensivos después de determinada cifra. Los números decimales infinitos pueden ser periódicos y no periódicos.
Números decimales infinitos periódicos: Son decimales en los que algunas de sus cifras decimales (o todas sus cifras decimales) se repiten con la misma frecuencia (o lo que es lo mismo se repiten con cierto periodo). Por ejemplo 1,222222... Se repite el 2.
0,1735353535... se repite el 35. Estos números siempre resultan de la división entre dos números enteros (siempre que el divisor sea diferente de cero).
Números decimales infinitos no periódicos: En estos números sus cifras decimales no se repiten con ningún tipo de periodicidad. Por ejemplo 4,25674136..., 0,0254785... . Estos números resultan de las raíces no exactas.
Entonces podemos concluir que a los racionales también pertenecen los decimales finitos y los decimales infinitos periódicos y que a los irracionales pertenecen también los decimales infinitos no periódicos.
PORCENTAJES:
Es otra forma de escribir un decimal, Para convertir a porcentaje se debe multiplicar el decimal por cien y colocar el símbolo %.
Para convertir a decimal se debe dividir el número en porcentaje entre cien y se debe quitar el símbolo de %.
f. NÚMEROS REALES. Están formados por la suma de los racionales más los irracionales. Son todos los números con los cuales vamos estudiar en matemáticas generales. Los matemáticos le asignaron la letra lR.. Todos los campos numéricos anteriores pertenecen a los números reales.
g. NÚMEROS IMAGINARIOS: A estos números pertenece la raíz par de todo número negativo. Se distinguen por la letra I. Por ejemplo . Si dices que te digo que no hay un número que multiplicado por sí mismo dos veces (y más general un número par de veces) de cómo resultado un número negativo. Para solucionar este problema y poder operar con este tipo de números nacieron los números imaginarios en los cuales se define: , y entonces la raíz par de cualquier número negativo se puede escribir en términos de i. Por ejemplo.
h. NÚMEROS COMPLEJOS: Están formados por la suma de los reales más. los imaginarios. A ellos pertenecen todos los campos numéricos. Se simbolizan con la letra C..
Ya que has entendido cada uno de los campos numéricos puedes dar respuesta a las siguientes afirmaciones.
como trabajar ecuaciones
PROBLEMAS QUE SE RESUELVEN USANDO ECUACIONES DE SEGUNDO GRADO
Cuando resolvemos UN problema mediante el uso de ecuaciones de segundo grado, debemos de tener en cuenta cual de Las raíces nos conduce a la solución del problema, puesto que al obtener dos raíces, es posible que Las dos sean solución del problema, por eso debemos de recurrir a Las condiciones que plantea el problema, pues es posible que solo una de Las dos cumpla la condición ó puede ser posible que Las dos cumplan, pues de no serlo así el problema no tendría solución, miremos algunos ejemplos.
Ejemplo 1. UN padre tiene 54 años y Su hijo 12años. ¿ Cuántos años hace que la edad del padre fue el cuadrado de la edad del hijo ?.
Solución : Llamemos X a la pregunta ¿ Cuántos años hace?. Luego planteamos que la edad del padre hace X años era de 54 - X, pero entonces el hijo tenía 12 - X. Por tanto el modelo según la condición que da el problema es :
Cuando resolvemos UN problema mediante el uso de ecuaciones de segundo grado, debemos de tener en cuenta cual de Las raíces nos conduce a la solución del problema, puesto que al obtener dos raíces, es posible que Las dos sean solución del problema, por eso debemos de recurrir a Las condiciones que plantea el problema, pues es posible que solo una de Las dos cumpla la condición ó puede ser posible que Las dos cumplan, pues de no serlo así el problema no tendría solución, miremos algunos ejemplos.
Ejemplo 1. UN padre tiene 54 años y Su hijo 12años. ¿ Cuántos años hace que la edad del padre fue el cuadrado de la edad del hijo ?.
Solución : Llamemos X a la pregunta ¿ Cuántos años hace?. Luego planteamos que la edad del padre hace X años era de 54 - X, pero entonces el hijo tenía 12 - X. Por tanto el modelo según la condición que da el problema es :
para trabajar
Don Wilson construye tanques para una empresa de químicos que los requiere en forma cilíndrica y con base pero sin tapa. En su construcción emplea una lámina rectangular y otra circular como se muestra en la figura.
1. De acuerdo con la figura podemos decir que:
A. X es el radio de la base y Y es la altura del cilindro.
B. Y es el radio de la base y X es la altura del cilindro.
C. X es el diámetro de la base y Y es la altura del cilindro.
D. 2πX es la base del rectángulo y Y es la altura del cilindro.
2.
El cliente le solicita a Don Wilson un tanque de 2 m de radio y 2 m de altura. Para construir este tanque se requiere:
A. 12π m2 de lámina
B. 8π m2 de lámina
C. 4π m2 de lámina
D. 8π m2 + 4 πm2 de láminas rectangular y circular respectivamente.
3.
Si Don Wilson cuenta para construir este tanque una sola lámina cuadrada sin cortar de 30π m2 , que tiene de ancho 4π m, podría construir:
A. Un tanque y le queda lámina para el cuerpo de un segundo tanque.
B. Dos tanques.
C. Dos tanques y le queda lámina para la base de al menos un tercer tanque.
D. Dos tanques y le queda lámina para el cuerpo de un tercer tanque.
4. Don Wilson dedujo una fórmula para calcular la lámina necesaria en tanques de igual radio y altura. Esta fórmula es:
A. 5 π X2
B. 4 π X2
C. 3 π X2
D. 2 π X2
5. Si el radio fuera igual a la altura, podríamos afirmar que el volumen es:
A. π X3
B. 2π X3
C. 3π X3
D. 4πX3
6.
Si duplicamos X dejando Y constante, entonces la capacidad del tanque:
A. Se duplicará porque el volumen está en proporción directa al radio.
B. Se cuadruplicará porque la base se cuadruplica y la altura está constante.
C. Se triplicará porque la base se triplica.
D. Permanecerá constante porque la base no afecta el volumen.
7. Si duplicamos X e Y simultáneamente, entonces la cantidad de lámina:
A. . Se duplicará porque el área está en proporción directa al radio
B. Se cuadruplicará porque el área de la base y el área lateral se cuadruplica.
C. Se triplicará porque la base se triplica.
D. Permanecerá constante porque la base no afecta al área total.
8.
Si en un momento dado Don Wilson cuenta con dos tipos de láminas rectangulares, la primera de medidas A de ancho por B de alto donde A > B y la segunda lámina de C de ancho por D de alto donde C > D >A, también se ha determinado que D=πB. El mayor tanque cilíndrico que Don Wilson podría construir utilizando ambas láminas rectangulares es uno de volumen:
A. π B2C
B. π B2C/4
C. π ABC
D. 2 π ABC
9.
El costo de la lámina del cuerpo del tanque tiene un costo de $a por m2. y la base cuesta un 50% más (incluyendo costos de material perdido en el corte). El costo de un tanque de igual radio y altura es:
A. 3aπX2
B. 3,5(aπX2)
C. 3.5(aπX2+2aπX2)
D. 1.5aπX2+2aπX
Otra empresa le pide a Don Wilson tanques con las mismas características, aunque esta vez con tapa.
10.
Esta empresa le solicita a Don Wilson un tanque de 2 m de radio y 2 m de altura. Para construir este tanque se requiere:
A. 16π m2 de lámina
B. 8π m2 de lámina
C. 4π m2 de lámina
D. 8π m2 + 8πm2 de láminas rectangular y circular respectivamente.
11.
Si Don Wilson para construir este tanque cuenta con una sola lámina sin cortar de 30π m2 , en la cual uno de los lados tiene las dimensiones de 4π m , podría construir:
A.
Un tanque y le queda lámina para el cuerpo de un segundo tanque.
B.
Dos tanques.
C. .Dos tanques y le queda lámina para varias bases o tapas para otros tanques.
D.
Dos tanques y le queda lámina para el cuerpo de un tercer tanque.
12. Don Wilson dedujo una fórmula para calcular la lámina necesaria en tanques de igual radio y altura. Esta fórmula es:
A. 5 π X2
B. 4 π X2
C. 3 π X2
D. 2 π X2
13. El costo de la lámina del cuerpo del tanque tiene un costo de $a por m2. y tanto la tapa como la base cuesta un 50% más (incluyendo costos de material perdido en el corte). El costo de un tanque de igual radio y altura es:
A. 3aπX2
B. 3,5(aπX2)
C. 5aπX2
D. 5aπX2+2πX2
14. Si el radio fuera igual a la altura, podríamos afirmar que el volumen es:
A. π X3
B. 2π X3
C. 3π X3
D. 4πX3
15. Si duplicamos X e Y simultáneamente, entonces la cantidad de lámina:
A. Se duplicará porque el área está en proporción directa al radio
B. Se cuadruplicará porque el área de la base, el área de la tapa y el área lateral se cuadruplica.
C. Se triplicará porque la base se triplica.
D. Permanecerá constante porque la base no afecta al área total.
16.
Si en un momento dado Don Wilson cuenta con tres tipos de láminas rectangulares, las dos primeras de medidas A de ancho por B de alto donde A > B y la segunda lámina de C de ancho por D de alto donde C > D >A, también se ha determinado que D=πB. El mayor tanque cilíndrico que Don Wilson podría construir utilizando las tres láminas rectangulares es uno de volumen:
A. π B2C
B. π B2C/4
C. π ABC
D. 2 π ABC
1. De acuerdo con la figura podemos decir que:
A. X es el radio de la base y Y es la altura del cilindro.
B. Y es el radio de la base y X es la altura del cilindro.
C. X es el diámetro de la base y Y es la altura del cilindro.
D. 2πX es la base del rectángulo y Y es la altura del cilindro.
2.
El cliente le solicita a Don Wilson un tanque de 2 m de radio y 2 m de altura. Para construir este tanque se requiere:
A. 12π m2 de lámina
B. 8π m2 de lámina
C. 4π m2 de lámina
D. 8π m2 + 4 πm2 de láminas rectangular y circular respectivamente.
3.
Si Don Wilson cuenta para construir este tanque una sola lámina cuadrada sin cortar de 30π m2 , que tiene de ancho 4π m, podría construir:
A. Un tanque y le queda lámina para el cuerpo de un segundo tanque.
B. Dos tanques.
C. Dos tanques y le queda lámina para la base de al menos un tercer tanque.
D. Dos tanques y le queda lámina para el cuerpo de un tercer tanque.
4. Don Wilson dedujo una fórmula para calcular la lámina necesaria en tanques de igual radio y altura. Esta fórmula es:
A. 5 π X2
B. 4 π X2
C. 3 π X2
D. 2 π X2
5. Si el radio fuera igual a la altura, podríamos afirmar que el volumen es:
A. π X3
B. 2π X3
C. 3π X3
D. 4πX3
6.
Si duplicamos X dejando Y constante, entonces la capacidad del tanque:
A. Se duplicará porque el volumen está en proporción directa al radio.
B. Se cuadruplicará porque la base se cuadruplica y la altura está constante.
C. Se triplicará porque la base se triplica.
D. Permanecerá constante porque la base no afecta el volumen.
7. Si duplicamos X e Y simultáneamente, entonces la cantidad de lámina:
A. . Se duplicará porque el área está en proporción directa al radio
B. Se cuadruplicará porque el área de la base y el área lateral se cuadruplica.
C. Se triplicará porque la base se triplica.
D. Permanecerá constante porque la base no afecta al área total.
8.
Si en un momento dado Don Wilson cuenta con dos tipos de láminas rectangulares, la primera de medidas A de ancho por B de alto donde A > B y la segunda lámina de C de ancho por D de alto donde C > D >A, también se ha determinado que D=πB. El mayor tanque cilíndrico que Don Wilson podría construir utilizando ambas láminas rectangulares es uno de volumen:
A. π B2C
B. π B2C/4
C. π ABC
D. 2 π ABC
9.
El costo de la lámina del cuerpo del tanque tiene un costo de $a por m2. y la base cuesta un 50% más (incluyendo costos de material perdido en el corte). El costo de un tanque de igual radio y altura es:
A. 3aπX2
B. 3,5(aπX2)
C. 3.5(aπX2+2aπX2)
D. 1.5aπX2+2aπX
Otra empresa le pide a Don Wilson tanques con las mismas características, aunque esta vez con tapa.
10.
Esta empresa le solicita a Don Wilson un tanque de 2 m de radio y 2 m de altura. Para construir este tanque se requiere:
A. 16π m2 de lámina
B. 8π m2 de lámina
C. 4π m2 de lámina
D. 8π m2 + 8πm2 de láminas rectangular y circular respectivamente.
11.
Si Don Wilson para construir este tanque cuenta con una sola lámina sin cortar de 30π m2 , en la cual uno de los lados tiene las dimensiones de 4π m , podría construir:
A.
Un tanque y le queda lámina para el cuerpo de un segundo tanque.
B.
Dos tanques.
C. .Dos tanques y le queda lámina para varias bases o tapas para otros tanques.
D.
Dos tanques y le queda lámina para el cuerpo de un tercer tanque.
12. Don Wilson dedujo una fórmula para calcular la lámina necesaria en tanques de igual radio y altura. Esta fórmula es:
A. 5 π X2
B. 4 π X2
C. 3 π X2
D. 2 π X2
13. El costo de la lámina del cuerpo del tanque tiene un costo de $a por m2. y tanto la tapa como la base cuesta un 50% más (incluyendo costos de material perdido en el corte). El costo de un tanque de igual radio y altura es:
A. 3aπX2
B. 3,5(aπX2)
C. 5aπX2
D. 5aπX2+2πX2
14. Si el radio fuera igual a la altura, podríamos afirmar que el volumen es:
A. π X3
B. 2π X3
C. 3π X3
D. 4πX3
15. Si duplicamos X e Y simultáneamente, entonces la cantidad de lámina:
A. Se duplicará porque el área está en proporción directa al radio
B. Se cuadruplicará porque el área de la base, el área de la tapa y el área lateral se cuadruplica.
C. Se triplicará porque la base se triplica.
D. Permanecerá constante porque la base no afecta al área total.
16.
Si en un momento dado Don Wilson cuenta con tres tipos de láminas rectangulares, las dos primeras de medidas A de ancho por B de alto donde A > B y la segunda lámina de C de ancho por D de alto donde C > D >A, también se ha determinado que D=πB. El mayor tanque cilíndrico que Don Wilson podría construir utilizando las tres láminas rectangulares es uno de volumen:
A. π B2C
B. π B2C/4
C. π ABC
D. 2 π ABC
martes, 31 de agosto de 2010
para la proxima clase realizar:
de la pag 171 realiza los ejercios correspondientes .
ejercicio 106 los cuales contiene 134 problemas factorables .
realizar los pares pero si desides ejecutar toda la miscelanea tendras una nota adicional
ejercicio 106 los cuales contiene 134 problemas factorables .
realizar los pares pero si desides ejecutar toda la miscelanea tendras una nota adicional
martes, 3 de agosto de 2010
Verticales
1- La suma de los cuadrados de los catetos es igual
R=/ Hipotenusa
2- Todo numero elevado a potencia 0 es igual
3- El primer nombre del escritor del algebra es?
4- La suma de cada lado se define como
5- Cual es elnombre de la ecuacion
6- Que nombre recibe el poligono de 6 lados.
7- La inversa de la suma es
8- 7x7x7 Tiene como base
9- Una igualdad de dos razones se le conoce como
10-LxL Es la formula parfa hallar
Horizontales
1- Raiz cuadrada de cero
2- La medida de los angulos se da
3- 2 x -4 =
4- Un Angulo menor de 90° Se le conoce como
5- El angulo de 90° Grados se le conoce como
6- El nombre del poligono de 5 lados es
7- 3x3x3x3 tiene como exponente
8- La letra U en las operaciones de los conujntos se reocnoce como
9- "Z" Pertenece a los conjuntos de los
10- Para que poligonos se emplea esta formula

martes, 13 de julio de 2010
Problemas de ecuaciones de primer grado
Esquema a seguir para resolver problemas de ecuaciones
Leer y comprender el enunciado
Designar la incógnita
Plantear la ecuación
Resolver la ecuación
Discusión e interpretación de los resultados
Leer y comprender el enunciado
Designar la incógnita
Plantear la ecuación
Resolver la ecuación
Discusión e interpretación de los resultados
martes, 8 de junio de 2010
Funcion Absoluta
Funcion Cuadratica
En matemáticas una función cuadrática o función de segundo grado es una función polinómica que se define mediante un polinomio de segundo grado como:

donde a, b y c son constantes y a es distinto de 0.
La representación gráfica en el plano XY haciendo:

es una parábola vertical, orientada hacia arriba o hacia abajo según el signo de a.
Algunas Graficas De Funciones!
Funcion Cuadratica:

Funcion Lineal:


donde a, b y c son constantes y a es distinto de 0.
La representación gráfica en el plano XY haciendo:

es una parábola vertical, orientada hacia arriba o hacia abajo según el signo de a.
Algunas Graficas De Funciones!
Funcion Cuadratica:

Funcion Lineal:

Función polinómica
martes, 1 de junio de 2010
ECUACION LINEAL !
Ecuacion lineal es un planteamiento de igualdad, involucrando una o más variables a la primera potencia, que no contiene productos entre las variables, es decir, una ecuación que involucra solamente sumas y restas de una variable a la primera potencia. En el sistema cartesiano representan rectas.
Ejemplo
* Y = 4 x -6



Ejercicios
* Y= 6 x - 2/3
* Y= 5 x - 4
*Y= 4 x +3/6
G.D.O.C.
martes, 4 de mayo de 2010
Descartes
Biografia
Biografía
Infancia y adolescencia
René Descartes nació el 31 de marzo de 1596 en La Haye en Touraine, cerca de Poitiers. Desde 1967 La Haye se llama Descartes en honor al filósofo, que fue el tercer hijo del jurista Joachim Descartes, noble de toga, y de Jeanne Brochard. Aunque René pensaba que su madre murió al nacer él, lo cierto es que murió un año después, durante el parto de un hermano que tampoco sobrevivió. Tras la muerte de su madre, él y sus 2 hermanos fueron educados por su abuela, pues su padre, consejero del Parlamento de Bretaña, se ausentaba cada 2 años por largas temporadas, y acabó dejando atrás a sus hijos al contraer nuevas nupcias con una doncella inglesa.
Educación
La educación en la Flèche le proporcionó, durante los cinco primeros años, una sólida introducción a la cultura clásica, habiendo aprendido latín y griego en la lectura de autores como Cicerón, Horacio y Virgilio, por un lado, y Homero, Píndaro y Platón, por el otro. El resto de la enseñanza estaba basada principalmente en textos filosóficos de Aristóteles (Organon, Metafísica, Ética a Nicómaco), acompañados por comentarios de jesuitas (Suárez, Fonseca, Toledo, quizá Vitoria) y otros autores españoles (Cayetano). Conviene destacar que Aristóteles era entonces el autor de referencia para el estudio, tanto de la física, como de la biología. El plan de estudios incluía también una introducción a las matemáticas (Clavius), tanto puras como aplicadas: astronomía, música, arquitectura. Siguiendo una extendida práctica medieval y clásica, en esta escuela los estudiantes se ejercitaban constantemente en la discusión () (Cfr. Gaukroger, quien toma en cuenta la Ratio studiorum: el plan de estudios que aplicaban las instituciones jesuíticas).
Registro de graduación de Descartes en el Collège Royal Henry-Le-Grand, La Flèche, 1616.La universidad
A los 18 años de edad, René Descartes ingresó a la Universidad de Poitiers para estudiar derecho y algo de medicina. Para 1616 Descartes cuenta con los grados de bachiller y licenciado. Descartes fue siempre un alumno sobresaliente y fue gracias al gran afecto de algunos de sus profesores lo que hizo que René pudiera visitar los laboratorios de la universidad con asiduidad.
Etapa investigadora
René Descartes en su escritorio.En 1619, en Breda, conoció a Isaac Beeckman, quien intentaba desarrollar una teoría física corpuscularista, muy basada en conceptos matemáticos. El contacto con Beeckman estimuló en gran medida el interés de Descartes por las matemática y la física. Pese a los constantes viajes que realizó en esta época, Descartes no dejó de formarse y en 1620 conoció en Ulm al entonces famoso maestro calculista alemán Johann Faulhaber. Él mismo refiere que, inspirado por una serie de sueños, en esta época vislumbró la posibilidad de desarrollar una «ciencia maravillosa». El hecho es que, probablemente estimulado por estos contactos, Descartes descubre el teorema denominado de Euler sobre los poliedros.
A pesar de discurrir sobre los temas anteriores, Descartes no publica entonces ninguno de estos resultados. Durante su estancia más larga en París, Descartes reafirma relaciones que había establecido a partir de 1622 con otros intelectuales, como Marin Mersenne y Guez de Balzac, así como con un círculo conocido como «Los libertinos». En esta época sus amigos propagan su reputación, hasta el punto de que su casa se convirtió entonces en un punto de reunión para quienes gustaban intercambiar ideas y discutir. Con todo ello su vida parece haber sido algo agitada, pues en 1628 libra un duelo, tras el cual comentó que «no he hallado una mujer cuya belleza pueda compararse a la de la verdad». El año siguiente, con la intención de dedicarse por completo al estudio, se traslada definitivamente a los Países Bajos, donde llevaría una vida modesta y tranquila, aunque cambiando de residencia constantemente para mantener oculto su paradero. Descartes permanece allí hasta 1649, viajando sin embargo en una ocasión a Dinamarca y en tres a Francia.
La preferencia de Descartes por Holanda parece haber sido bastante acertada, pues mientras en Francia muchas cosas podrían distraerlo y había escasa tolerancia, las ciudades holandesas estaban en paz, florecían gracias al comercio y grupos de burgueses potenciaban las ciencias fundándose la academia de Ámsterdam en 1632. Entre tanto, el centro de Europa se desgarraba en la Guerra de los Treinta Años, que terminaría en 1648. Enunció las leyes de refracción y reflexión de la luz y fundó la geometría analítica.
Fallecimiento
Descartes en la Corte de la reina Cristina de Suecia (detalle), Pierre Louis Dumesnil. Museo nacional de Versailles.
La tumba de Descartes (en el centro), con vista detallada de la inscripción, en la iglesia de Saint-Germain-des-Prés, París.En septiembre de 1649 la Reina Cristina de Suecia le llamó a Estocolmo. Allí murió de una neumonía el 11 de febrero de 1650. Falleció a los 53 años de edad.
Actualmente se pone en duda si la causa de su muerte fue la neumonía. En 1980, el historiador y médico alemán Eike Pies halló en la Universidad de Leiden una carta secreta del médico de la corte que atendió a Descartes, el holandés Johan Van Wullen, en la que describía al detalle su agonía. Curiosamente, los síntomas presentados —náuseas, vómitos, escalofríos— no eran propios de una neumonía. Tras consultar a varios patólogos, Pies concluyó en su libro El homicidio de Descartes, documentos, indicios, pruebas, que la muerte se debía a envenenamiento por arsénico. La carta secreta fue enviada a un antepasado del escritor, el holandés Willem Pies.
En el año de 1676 se exhumaron los restos de Descartes; colocados en un ataúd de cobre se trasladaron a París para sepultarlos en la iglesia de Sainte-Geneviève-du-Mont; movidos nuevamente durante el transcurso de la Revolución francesa, los restos fueron colocados en el Panthéon, la basílica dedicada a los grandes hombres de la nación francesa; nuevamente, en 1819, los restos de René Descartes cambiaron de sitio de reposo siendo llevados esta vez a la Iglesia de Saint-Germain-des-Prés donde actualmente se encuentran.
En 1935 se decidió en su honor llamar «Descartes» a un cráter lunar.[1]
Biografía
Infancia y adolescencia
René Descartes nació el 31 de marzo de 1596 en La Haye en Touraine, cerca de Poitiers. Desde 1967 La Haye se llama Descartes en honor al filósofo, que fue el tercer hijo del jurista Joachim Descartes, noble de toga, y de Jeanne Brochard. Aunque René pensaba que su madre murió al nacer él, lo cierto es que murió un año después, durante el parto de un hermano que tampoco sobrevivió. Tras la muerte de su madre, él y sus 2 hermanos fueron educados por su abuela, pues su padre, consejero del Parlamento de Bretaña, se ausentaba cada 2 años por largas temporadas, y acabó dejando atrás a sus hijos al contraer nuevas nupcias con una doncella inglesa.
Educación
La educación en la Flèche le proporcionó, durante los cinco primeros años, una sólida introducción a la cultura clásica, habiendo aprendido latín y griego en la lectura de autores como Cicerón, Horacio y Virgilio, por un lado, y Homero, Píndaro y Platón, por el otro. El resto de la enseñanza estaba basada principalmente en textos filosóficos de Aristóteles (Organon, Metafísica, Ética a Nicómaco), acompañados por comentarios de jesuitas (Suárez, Fonseca, Toledo, quizá Vitoria) y otros autores españoles (Cayetano). Conviene destacar que Aristóteles era entonces el autor de referencia para el estudio, tanto de la física, como de la biología. El plan de estudios incluía también una introducción a las matemáticas (Clavius), tanto puras como aplicadas: astronomía, música, arquitectura. Siguiendo una extendida práctica medieval y clásica, en esta escuela los estudiantes se ejercitaban constantemente en la discusión () (Cfr. Gaukroger, quien toma en cuenta la Ratio studiorum: el plan de estudios que aplicaban las instituciones jesuíticas).
Registro de graduación de Descartes en el Collège Royal Henry-Le-Grand, La Flèche, 1616.La universidad
A los 18 años de edad, René Descartes ingresó a la Universidad de Poitiers para estudiar derecho y algo de medicina. Para 1616 Descartes cuenta con los grados de bachiller y licenciado. Descartes fue siempre un alumno sobresaliente y fue gracias al gran afecto de algunos de sus profesores lo que hizo que René pudiera visitar los laboratorios de la universidad con asiduidad.
Etapa investigadora
René Descartes en su escritorio.En 1619, en Breda, conoció a Isaac Beeckman, quien intentaba desarrollar una teoría física corpuscularista, muy basada en conceptos matemáticos. El contacto con Beeckman estimuló en gran medida el interés de Descartes por las matemática y la física. Pese a los constantes viajes que realizó en esta época, Descartes no dejó de formarse y en 1620 conoció en Ulm al entonces famoso maestro calculista alemán Johann Faulhaber. Él mismo refiere que, inspirado por una serie de sueños, en esta época vislumbró la posibilidad de desarrollar una «ciencia maravillosa». El hecho es que, probablemente estimulado por estos contactos, Descartes descubre el teorema denominado de Euler sobre los poliedros.
A pesar de discurrir sobre los temas anteriores, Descartes no publica entonces ninguno de estos resultados. Durante su estancia más larga en París, Descartes reafirma relaciones que había establecido a partir de 1622 con otros intelectuales, como Marin Mersenne y Guez de Balzac, así como con un círculo conocido como «Los libertinos». En esta época sus amigos propagan su reputación, hasta el punto de que su casa se convirtió entonces en un punto de reunión para quienes gustaban intercambiar ideas y discutir. Con todo ello su vida parece haber sido algo agitada, pues en 1628 libra un duelo, tras el cual comentó que «no he hallado una mujer cuya belleza pueda compararse a la de la verdad». El año siguiente, con la intención de dedicarse por completo al estudio, se traslada definitivamente a los Países Bajos, donde llevaría una vida modesta y tranquila, aunque cambiando de residencia constantemente para mantener oculto su paradero. Descartes permanece allí hasta 1649, viajando sin embargo en una ocasión a Dinamarca y en tres a Francia.
La preferencia de Descartes por Holanda parece haber sido bastante acertada, pues mientras en Francia muchas cosas podrían distraerlo y había escasa tolerancia, las ciudades holandesas estaban en paz, florecían gracias al comercio y grupos de burgueses potenciaban las ciencias fundándose la academia de Ámsterdam en 1632. Entre tanto, el centro de Europa se desgarraba en la Guerra de los Treinta Años, que terminaría en 1648. Enunció las leyes de refracción y reflexión de la luz y fundó la geometría analítica.
Fallecimiento
Descartes en la Corte de la reina Cristina de Suecia (detalle), Pierre Louis Dumesnil. Museo nacional de Versailles.
La tumba de Descartes (en el centro), con vista detallada de la inscripción, en la iglesia de Saint-Germain-des-Prés, París.En septiembre de 1649 la Reina Cristina de Suecia le llamó a Estocolmo. Allí murió de una neumonía el 11 de febrero de 1650. Falleció a los 53 años de edad.
Actualmente se pone en duda si la causa de su muerte fue la neumonía. En 1980, el historiador y médico alemán Eike Pies halló en la Universidad de Leiden una carta secreta del médico de la corte que atendió a Descartes, el holandés Johan Van Wullen, en la que describía al detalle su agonía. Curiosamente, los síntomas presentados —náuseas, vómitos, escalofríos— no eran propios de una neumonía. Tras consultar a varios patólogos, Pies concluyó en su libro El homicidio de Descartes, documentos, indicios, pruebas, que la muerte se debía a envenenamiento por arsénico. La carta secreta fue enviada a un antepasado del escritor, el holandés Willem Pies.
En el año de 1676 se exhumaron los restos de Descartes; colocados en un ataúd de cobre se trasladaron a París para sepultarlos en la iglesia de Sainte-Geneviève-du-Mont; movidos nuevamente durante el transcurso de la Revolución francesa, los restos fueron colocados en el Panthéon, la basílica dedicada a los grandes hombres de la nación francesa; nuevamente, en 1819, los restos de René Descartes cambiaron de sitio de reposo siendo llevados esta vez a la Iglesia de Saint-Germain-des-Prés donde actualmente se encuentran.
En 1935 se decidió en su honor llamar «Descartes» a un cráter lunar.[1]
Que es el plano cartesiano
Historia:
Se denominan coordenadas cartesianas en honor a René Descartes (1596-1650), el célebre filósofo y matemático francés que quiso fundamentar su pensamiento filosófico en la necesidad de tomar un «punto de partida» sobre el que edificar todo el conocimiento.
Como creador de la geometría analítica, también comienza tomando un «punto de partida»: el sistema de referencia cartesiano, para poder representar la geometría plana tomando como referencia dos rectas perpendiculares entre sí, que se cortan en un punto denominado «origen de coordenadas», ideando las denominadas coordenadas cartesianas
Se denominan coordenadas cartesianas en honor a René Descartes (1596-1650), el célebre filósofo y matemático francés que quiso fundamentar su pensamiento filosófico en la necesidad de tomar un «punto de partida» sobre el que edificar todo el conocimiento.
Como creador de la geometría analítica, también comienza tomando un «punto de partida»: el sistema de referencia cartesiano, para poder representar la geometría plana tomando como referencia dos rectas perpendiculares entre sí, que se cortan en un punto denominado «origen de coordenadas», ideando las denominadas coordenadas cartesianas
Que es el plano cartesiano
Historia:
Se denominan coordenadas cartesianas en honor a René Descartes (1596-1650), el célebre filósofo y matemático francés que quiso fundamentar su pensamiento filosófico en la necesidad de tomar un «punto de partida» sobre el que edificar todo el conocimiento.
Como creador de la geometría analítica, también comienza tomando un «punto de partida»: el sistema de referencia cartesiano, para poder representar la geometría plana tomando como referencia dos rectas perpendiculares entre sí, que se cortan en un punto denominado «origen de coordenadas», ideando las denominadas coordenadas cartesianas
Se denominan coordenadas cartesianas en honor a René Descartes (1596-1650), el célebre filósofo y matemático francés que quiso fundamentar su pensamiento filosófico en la necesidad de tomar un «punto de partida» sobre el que edificar todo el conocimiento.
Como creador de la geometría analítica, también comienza tomando un «punto de partida»: el sistema de referencia cartesiano, para poder representar la geometría plana tomando como referencia dos rectas perpendiculares entre sí, que se cortan en un punto denominado «origen de coordenadas», ideando las denominadas coordenadas cartesianas
Que es un escalar ?
Definicion :
Se denomina escalar a los números reales, complejos o racionales que sirven para describir un fenómeno físico con magnitud, pero sin las características vectoriales de dirección o sentido. Formalmente es un tensor de rango cero.
En términos matemáticos, se llama escalar a los elementos de un cuerpo (en algunos casos también a los elementos de un anillo), generalmente números, y en particular se usa cuando se quiere distinguirlos claramente de los vectores en el álgebra lineal y en cualquier rama que use módulos o espacios vectoriales.
Se denomina escalar a los números reales, complejos o racionales que sirven para describir un fenómeno físico con magnitud, pero sin las características vectoriales de dirección o sentido. Formalmente es un tensor de rango cero.
En términos matemáticos, se llama escalar a los elementos de un cuerpo (en algunos casos también a los elementos de un anillo), generalmente números, y en particular se usa cuando se quiere distinguirlos claramente de los vectores en el álgebra lineal y en cualquier rama que use módulos o espacios vectoriales.
Función compuesta
En matemática, una función compuesta es una función formada por la composición o aplicación sucesiva de otras dos funciones. Para ello, se aplica sobre el argumento la función más próxima al mismo, y al resultado del cálculo anterior se le aplica finalmente la función restante.
Formalmente, dadas dos funciones f: X → Y y g: Y → Z, donde la imagen de f está contenida en el dominio de g, se define la función composición (g ο f ): X → Z como (g ο f)(x) = g (f(x)), para todos los elementos x de X.


La función compuesta de g y de f que expresamos:


Formalmente, dadas dos funciones f: X → Y y g: Y → Z, donde la imagen de f está contenida en el dominio de g, se define la función composición (g ο f ): X → Z como (g ο f)(x) = g (f(x)), para todos los elementos x de X.
x-y-z
X-F(x)-G(f(x))
A g ο f se le llama composición de f y g. Nótese que se nombra no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.
Ejemplo:
sean las funciones:
Ejemplo:
sean las funciones:


La función compuesta de g y de f que expresamos:

La interpretación de (f o g) aplicada a la variable x significa que primero tenemos que aplicar g a x, con lo que obtendríamos un valor de paso :

y después aplicamos f a z para obtener:

Funcion lineal
Se denomina transformación lineal, función lineal o aplicación lineal a toda aplicación cuyo dominio y codominio sean espacios vectoriales que cumpla la siguiente definición:
Sean V y W espacios vectoriales sobre el mismo espacio o campo K, y T una función de V en W. T es una transformación lineal si para todo par de vectores u y v pertenecientes a V y para todo escalar k perteneciente a K, se satisface que:
1. T(u+v)= T(u)+ T(u)
2. T(ku) = kT (u)donde k es un escalar
Sean V y W espacios vectoriales sobre el mismo espacio o campo K, y T una función de V en W. T es una transformación lineal si para todo par de vectores u y v pertenecientes a V y para todo escalar k perteneciente a K, se satisface que:
1. T(u+v)= T(u)+ T(u)
2. T(ku) = kT (u)donde k es un escalar
Relaciones y funciones

RELACIONES y FUNCIONES
Hay casos en que no todos los pares ordenados de un producto cartesiano de dos conjuntos responden a una condición dada. Se llama relación entre los conjuntos A y B a un subconjunto del producto cartesiano A x B. Este puede estar formado por un solo par ordenado, varios o todos los que forman parte de A x B. Si establecemos una relación entre los elementos de un mismo conjunto, existen tres propiedades fundamentales que pueden cumplirse en esa relación: propiedad reflexiva, simétrica y transitiva.
Se llama función a una relación en la cual a cada elemento del conjunto de partida le corresponde sólo un elemento del conjunto de llegada.
martes, 20 de abril de 2010
Calculo Racional
El Cálculo relacional es un lenguaje de consulta que describe la respuesta deseada sobre una Base de datos sin especificar como obtenerla, a diferencia del Álgebra relacional que es de tipo procedural, el cálculo relacional es de tipo declarativo; pero siempre ambos métodos logran los mismos resultados
Clases de Cálculo Relacional
Cálculo Relacional basado en Tuplas. (TRC)
Cálculo Relacional basado en Dominios (DRC)
Cálculo Relacional basado en Tuplas. (TRC)
Una consulta en TRC es de la forma:
{T φ(T )}
donde T es una variable tipo tupla y φ(T ) es una fórmula que describe a T. El resultado de esta consulta, son todas las tuplas t para las cuales la fórmula es verdadera.
Cálculo Relacional basado en Dominios (DRC)
Está constituido con los mismos operadores que el calculo relacional de tuplas pero no hay tuplas sino variables dominio. Las expresiones del cálculo relacional de dominios son de la forma { (x, y, z, ...) / P(x, y, z, ...) }. Donde x, y, z representan las variables de dominio, P representa una fórmula compuesta de átomos (igual que en el CRT). Los átomos del cálculo relacional de dominios tienen una de las siguientes formas:
1. (x, y, z ) r, donde r es una relación con n atributos y x , y, z .son variables de dominio o constantes.
2. x y, donde x e y son variables de dominio y es un operador de comparación aritmética (>, <, =, ). Es necesario que los atributos x e y, tengan dominios cuyos miembros puedan compararse mediante .
3. x c, donde x es una variable de dominio, es un operador de comparación y c es una constante en el dominio del atributo x
Clases de Cálculo Relacional
Cálculo Relacional basado en Tuplas. (TRC)
Cálculo Relacional basado en Dominios (DRC)
Cálculo Relacional basado en Tuplas. (TRC)
Una consulta en TRC es de la forma:
{T φ(T )}
donde T es una variable tipo tupla y φ(T ) es una fórmula que describe a T. El resultado de esta consulta, son todas las tuplas t para las cuales la fórmula es verdadera.
Cálculo Relacional basado en Dominios (DRC)
Está constituido con los mismos operadores que el calculo relacional de tuplas pero no hay tuplas sino variables dominio. Las expresiones del cálculo relacional de dominios son de la forma { (x, y, z, ...) / P(x, y, z, ...) }. Donde x, y, z representan las variables de dominio, P representa una fórmula compuesta de átomos (igual que en el CRT). Los átomos del cálculo relacional de dominios tienen una de las siguientes formas:
1. (x, y, z ) r, donde r es una relación con n atributos y x , y, z .son variables de dominio o constantes.
2. x y, donde x e y son variables de dominio y es un operador de comparación aritmética (>, <, =, ). Es necesario que los atributos x e y, tengan dominios cuyos miembros puedan compararse mediante .
3. x c, donde x es una variable de dominio, es un operador de comparación y c es una constante en el dominio del atributo x
Calculo Diferencial
El cálculo diferencial, una rama de las matemáticas, es el estudio de cómo cambian las funciones cuando sus variables cambian. El principal objeto de estudio en el cálculo diferencial es la derivada. Una noción estrechamente relacionada es la de diferencial.
Desde el punto de vista matemático de las funciones y la geometría, la derivada de una función en un cierto punto es una medida de la tasa en la cual una función cambia conforme un argumento se modifica. Esto es, una derivada involucra, en términos matemáticos, una tasa de cambio. Una derivada es el cálculo de las pendientes instantáneas de f(x) en cada punto x. Esto se corresponde a las pendientes de las tangentes de la gráfica de dicha función en sus puntos (una tangente por punto); Las derivadas pueden ser utilizadas para conocer la concavidad de una función, sus intervalos de crecimiento, sus máximos y mínimos.
Desde el punto de vista matemático de las funciones y la geometría, la derivada de una función en un cierto punto es una medida de la tasa en la cual una función cambia conforme un argumento se modifica. Esto es, una derivada involucra, en términos matemáticos, una tasa de cambio. Una derivada es el cálculo de las pendientes instantáneas de f(x) en cada punto x. Esto se corresponde a las pendientes de las tangentes de la gráfica de dicha función en sus puntos (una tangente por punto); Las derivadas pueden ser utilizadas para conocer la concavidad de una función, sus intervalos de crecimiento, sus máximos y mínimos.
Propiedades De Las Raices
Las propiedades que estudiaremos a continuación se basan en:
a) La posibilidad de expresar una raíz en forma de potencia de exponente fraccionario.
b) Las propiedades de las potencias de exponente entero que hemos hecho extensivas a las de exponente fraccionario.
Propiedad fundamental
El resultado de una raíz no varia si multiplicamos o dividimos el índice y el exponente del radicando por un mismo número diferente de 0.
Raíz de una multiplicación
La raíz de una multiplicación es igual al producto de las raíces de los factores.
Raíz de una división
La raíz de una división es igual al cociente de las raíces del dividendo y del divisor.
Potencia de una raíz
Para elevar una raíz a una potencia se eleva el radicando a esta potencia.
Raíz de una raíz
La raíz de una raíz da como resultado otra raíz del mismo radicando y de índice igual al producto de dos índices.
a) La posibilidad de expresar una raíz en forma de potencia de exponente fraccionario.
b) Las propiedades de las potencias de exponente entero que hemos hecho extensivas a las de exponente fraccionario.
Propiedad fundamental
El resultado de una raíz no varia si multiplicamos o dividimos el índice y el exponente del radicando por un mismo número diferente de 0.
Raíz de una multiplicación
La raíz de una multiplicación es igual al producto de las raíces de los factores.
Raíz de una división
La raíz de una división es igual al cociente de las raíces del dividendo y del divisor.
Potencia de una raíz
Para elevar una raíz a una potencia se eleva el radicando a esta potencia.
Raíz de una raíz
La raíz de una raíz da como resultado otra raíz del mismo radicando y de índice igual al producto de dos índices.
Propiedades de la Potencia
La potenciación es una expresión matemática que incluye dos términos denominados: base a y exponente n.
Se escribe an, y se lee: «a elevado a n». Su definición varía según el conjunto numérico al que pertenezca el exponente:
Cuando el exponente es un número natural, equivale a multiplicar un número por sí mismo varias veces: el exponente determina la cantidad de veces.
Por ejemplo: .
cuando el exponente es un número entero negativo, equivale a la fracción inversa de la base pero con exponente positivo.
cuando el exponente es una fracción irreducible n/m, equivale a una raíz:
Cualquier número elevado a 0 equivale a 1, excepto el caso particular de 00 que, en principio, es una indefinición (ver cero).
La definición de potenciación puede extenderse a exponentes reales, complejos o incluso matriciales
Se escribe an, y se lee: «a elevado a n». Su definición varía según el conjunto numérico al que pertenezca el exponente:
Cuando el exponente es un número natural, equivale a multiplicar un número por sí mismo varias veces: el exponente determina la cantidad de veces.
Por ejemplo: .
cuando el exponente es un número entero negativo, equivale a la fracción inversa de la base pero con exponente positivo.
cuando el exponente es una fracción irreducible n/m, equivale a una raíz:
Cualquier número elevado a 0 equivale a 1, excepto el caso particular de 00 que, en principio, es una indefinición (ver cero).
La definición de potenciación puede extenderse a exponentes reales, complejos o incluso matriciales
Triangulo De Pascal
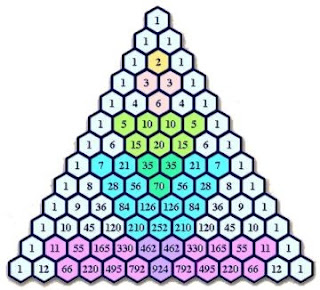
El triángulo de Pascal en matemáticas es un conjunto infinito de números enteros ordenados en forma de triángulo que expresan coeficientes binomiales. El interés del Triángulo de Pascal radica en su aplicación en álgebra y permite calcular de forma sencilla números combinatorios lo que sirve para aplicar el binomio de Newton.
martes, 13 de abril de 2010
Ecuacion Cuadratica
Consideremos la ecuación cuadrática general ax2 + bx + c = 0.
Se puede resolver al completar el cuadrado.
Analizando la raíz cuadrada, se llega a las siguientes conclusiones:
Si b2 es menor que − 4ac los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un numero complejo.
Si b2 es mayor que − 4ac obtendremos dos valores distintos de X reales.
Y si b2 es igual que − 4ac obtendremos dos valores de X reales e iguales.
Al término b2 − 4ac se le llama discriminante.
Se puede resolver al completar el cuadrado.
Analizando la raíz cuadrada, se llega a las siguientes conclusiones:
Si b2 es menor que − 4ac los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un numero complejo.
Si b2 es mayor que − 4ac obtendremos dos valores distintos de X reales.
Y si b2 es igual que − 4ac obtendremos dos valores de X reales e iguales.
Al término b2 − 4ac se le llama discriminante.
Valor Absoluto
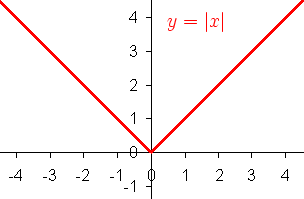
En matemática, el valor absoluto o módulo[1] de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de 3 y de -3.
El valor absoluto está relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.
El valor absoluto está relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.
Inecuaciones Irracionales
Las Palabras Claves Son :
ángulos | aplicaciones económicas | asíntotas | autoevaluación de matemáticas | bibliografía | circunferencia | concavidad | Cónicas | Continuidad | convexidad | coseno | Cramer | Crecimiento | curso cero | decrecimiento | derivada | determinantes | dominio | ecuaciones | ecuaciones irracionales | ecuaciones polinómicas | ecuaciones racionales | ejercicios para resolver | ejercicios resueltos | elipse | enlaces | fracciones | función exponencial | función logarítmica | función potencial | funciones reales | funciones trigonométricas | hipérbola | inecuaciones | inecuaciones irracionales | inecuaciones polinómicas | inecuaciones racionales | Límites | lineales | logaritmos | matemáticas básicas | matemáticas para economistas | matrices | máximo | método de Gauss | mínimo | Números complejos | números decimales | números enteros | números irracionales | números naturales | números racionales | Números reales | operaciones elementales | parábola | pendiente | potencias | puntos | puntos de inflexión | raíces | ramas parabólicas | rango | recta | regla de L´Hôpital | representación gráfica | seno | sistemas | tangente | trigonometría | Vectores
ángulos | aplicaciones económicas | asíntotas | autoevaluación de matemáticas | bibliografía | circunferencia | concavidad | Cónicas | Continuidad | convexidad | coseno | Cramer | Crecimiento | curso cero | decrecimiento | derivada | determinantes | dominio | ecuaciones | ecuaciones irracionales | ecuaciones polinómicas | ecuaciones racionales | ejercicios para resolver | ejercicios resueltos | elipse | enlaces | fracciones | función exponencial | función logarítmica | función potencial | funciones reales | funciones trigonométricas | hipérbola | inecuaciones | inecuaciones irracionales | inecuaciones polinómicas | inecuaciones racionales | Límites | lineales | logaritmos | matemáticas básicas | matemáticas para economistas | matrices | máximo | método de Gauss | mínimo | Números complejos | números decimales | números enteros | números irracionales | números naturales | números racionales | Números reales | operaciones elementales | parábola | pendiente | potencias | puntos | puntos de inflexión | raíces | ramas parabólicas | rango | recta | regla de L´Hôpital | representación gráfica | seno | sistemas | tangente | trigonometría | Vectores
martes, 6 de abril de 2010
INECUACIONES

Una inecuación es una expresión matemática la cual se caracteriza por tener los signos de desigualdad; Siendo una expresión algebraica nos da como resultado un conjunto en el cual la variable independiente puede tomar el valor cualesquiera de ese conjunto cumpliendo esta desigualdad; a este conjunto se le conoce como Intervalo.
Ejemplo
5x+3+2>8+4x
= 5x-4x>8-5
= x>3
Hitoria del calculo

Antiguidade
De acordo com Gauss, Arquimedes, o maior matemático da antigüidade, já apresentava idéias relacionadas ao Cálculo dois séculos antes de Cristo.Na Antiguidade, foram introduzidas algumas idéias do cálculo integral, embora não tenha havido um desenvolvimento dessas idéias de forma rigorosa e sistemática. A função básica do cálculo integral, calcular volumes e áreas, pode ser remontada ao Papiro Egípcio de Moscow (1800 a.C.), no qual um egípcio trabalhou o volume de um frustum piramidal. Eudoxus (408-355 a.C.) usou o método da exaustão para calcular áreas e volumes. Arquimedes (287-212 a.C.) levou essa idéia além, inventando a heurística, que se aproxima do cálculo integral. O método da exaustão foi redescoberto na China por Liu Hui no século III, que o usou para encontrar a área do círculo. O método também foi usado por Zu Chongzhi século V, para achar o volume de uma esfera.
Idade Média
Na Idade Média, o matemático indiano Aryabhata usou a noção infinitesimal em 499 d.C. expressando-a em um problema de astronomia na forma de uma equação diferencial básica. Essa equação levou Bhāskara II no século XII a desenvolver uma derivada prematura representado uma mudança infinitesimal, e ele desenvolveu também o que seria uma forma primitiva do "Teorema de Rolle".
No século XII, o matemático persa Sharaf al-Din al-Tusi descobriu a derivada de polinômios cúbicos, um resultado importante no cálculo diferencial. No século XIV, Madhava de Sangamagrama, juntamente com outros matemáticos-astrônomos da Escola Kerala de Astronomia e Matemática, descreveu casos especiais da Série de Taylor, que no texto são tratadas como Yuktibhasa.
Idade Moderna
Sir Isaac Newton aplicou o cálculo às suas leis do movimento e a outros conceitos matemáticos-físicos.No Idade Moderna, descobertas independentes no cálculo foram feitas no início do século XVII no Japão por matemáticos como Seki Kowa, que expandiu o método de exaustão. Na Europa, a segunda metade do século XVII foi uma época de grandes inovações. O Cálculo abriu novas oportunidades na física-matemática de resolver problemas muito antigos que até então não haviam sido solucionados. Muitos matemáticos contribuíram para essas descobertas, notavelmente John Wallis e Isaac Barrow. James Gregory proveu um caso especial do segundo teorema fundamental do cálculo em 1668.
Coube a Gottfried Wilhelm von Leibniz e a Isaac Newton recolher essas idéias e juntá-las em um corpo teórico que viria a constituir o cálculo. A ambos é atribuída a simultânea e independente invenção do cálculo. Leibnitz foi originalmente acusado de plagiar os trabalhos não publicados de Isaac Newton; hoje porém é considerado o inventor do cálculo, juntamente com Newton. Historicamente Newton foi o primeiro a aplicar o cálculo à física ao passo que Leibniz desenvolveu a notação utilizada até os dias de hoje. O argumento histórico para conferir aos dois a invenção do cálculo é que ambos chegaram de maneiras distintas ao teorema fundamental do cálculo.
Gottfried Wilhelm Leibniz: o inventor do cálculo, juntamente com Newton.Quando Newton e Leibniz publicaram seus resultados, houve uma grande controvérsia de qual matemático (e portanto que país: Inglaterra ou Alemanha) merecia o crédito. Newton derivou seus resultados primeiro, mas Leibniz publicou primeiro. Newton argumentou que Leibniz roubou idéias de seus escritos não publicados, que Newton à época compartilhara com alguns poucos membros da Sociedade Real. Esta controvérsia dividiu os matemáticos ingleses dos matemáticos alemães por muitos anos. Um exame cuidadoso dos escritos de Leibniz e Newton mostra que ambos chegaram a seus resultados independentemente, com Leibniz iniciando com integração e Newton com diferenciação. Nos dias de hoje tem-se que Newton e Leibniz descobriram o cálculo independentemente. Leibniz, porém, foi quem deu o nome cálculo à nova disciplina, Newton a chamara de "A ciência dos fluxos".
Desde o tempo de Leibniz e Newton, muitos matemáticos contribuíram
Suscribirse a:
Comentarios (Atom)















