El Cálculo relacional es un lenguaje de consulta que describe la respuesta deseada sobre una Base de datos sin especificar como obtenerla, a diferencia del Álgebra relacional que es de tipo procedural, el cálculo relacional es de tipo declarativo; pero siempre ambos métodos logran los mismos resultados
Clases de Cálculo Relacional
Cálculo Relacional basado en Tuplas. (TRC)
Cálculo Relacional basado en Dominios (DRC)
Cálculo Relacional basado en Tuplas. (TRC)
Una consulta en TRC es de la forma:
{T φ(T )}
donde T es una variable tipo tupla y φ(T ) es una fórmula que describe a T. El resultado de esta consulta, son todas las tuplas t para las cuales la fórmula es verdadera.
Cálculo Relacional basado en Dominios (DRC)
Está constituido con los mismos operadores que el calculo relacional de tuplas pero no hay tuplas sino variables dominio. Las expresiones del cálculo relacional de dominios son de la forma { (x, y, z, ...) / P(x, y, z, ...) }. Donde x, y, z representan las variables de dominio, P representa una fórmula compuesta de átomos (igual que en el CRT). Los átomos del cálculo relacional de dominios tienen una de las siguientes formas:
1. (x, y, z ) r, donde r es una relación con n atributos y x , y, z .son variables de dominio o constantes.
2. x y, donde x e y son variables de dominio y es un operador de comparación aritmética (>, <, =, ). Es necesario que los atributos x e y, tengan dominios cuyos miembros puedan compararse mediante .
3. x c, donde x es una variable de dominio, es un operador de comparación y c es una constante en el dominio del atributo x
martes, 20 de abril de 2010
Calculo Diferencial
El cálculo diferencial, una rama de las matemáticas, es el estudio de cómo cambian las funciones cuando sus variables cambian. El principal objeto de estudio en el cálculo diferencial es la derivada. Una noción estrechamente relacionada es la de diferencial.
Desde el punto de vista matemático de las funciones y la geometría, la derivada de una función en un cierto punto es una medida de la tasa en la cual una función cambia conforme un argumento se modifica. Esto es, una derivada involucra, en términos matemáticos, una tasa de cambio. Una derivada es el cálculo de las pendientes instantáneas de f(x) en cada punto x. Esto se corresponde a las pendientes de las tangentes de la gráfica de dicha función en sus puntos (una tangente por punto); Las derivadas pueden ser utilizadas para conocer la concavidad de una función, sus intervalos de crecimiento, sus máximos y mínimos.
Desde el punto de vista matemático de las funciones y la geometría, la derivada de una función en un cierto punto es una medida de la tasa en la cual una función cambia conforme un argumento se modifica. Esto es, una derivada involucra, en términos matemáticos, una tasa de cambio. Una derivada es el cálculo de las pendientes instantáneas de f(x) en cada punto x. Esto se corresponde a las pendientes de las tangentes de la gráfica de dicha función en sus puntos (una tangente por punto); Las derivadas pueden ser utilizadas para conocer la concavidad de una función, sus intervalos de crecimiento, sus máximos y mínimos.
Propiedades De Las Raices
Las propiedades que estudiaremos a continuación se basan en:
a) La posibilidad de expresar una raíz en forma de potencia de exponente fraccionario.
b) Las propiedades de las potencias de exponente entero que hemos hecho extensivas a las de exponente fraccionario.
Propiedad fundamental
El resultado de una raíz no varia si multiplicamos o dividimos el índice y el exponente del radicando por un mismo número diferente de 0.
Raíz de una multiplicación
La raíz de una multiplicación es igual al producto de las raíces de los factores.
Raíz de una división
La raíz de una división es igual al cociente de las raíces del dividendo y del divisor.
Potencia de una raíz
Para elevar una raíz a una potencia se eleva el radicando a esta potencia.
Raíz de una raíz
La raíz de una raíz da como resultado otra raíz del mismo radicando y de índice igual al producto de dos índices.
a) La posibilidad de expresar una raíz en forma de potencia de exponente fraccionario.
b) Las propiedades de las potencias de exponente entero que hemos hecho extensivas a las de exponente fraccionario.
Propiedad fundamental
El resultado de una raíz no varia si multiplicamos o dividimos el índice y el exponente del radicando por un mismo número diferente de 0.
Raíz de una multiplicación
La raíz de una multiplicación es igual al producto de las raíces de los factores.
Raíz de una división
La raíz de una división es igual al cociente de las raíces del dividendo y del divisor.
Potencia de una raíz
Para elevar una raíz a una potencia se eleva el radicando a esta potencia.
Raíz de una raíz
La raíz de una raíz da como resultado otra raíz del mismo radicando y de índice igual al producto de dos índices.
Propiedades de la Potencia
La potenciación es una expresión matemática que incluye dos términos denominados: base a y exponente n.
Se escribe an, y se lee: «a elevado a n». Su definición varía según el conjunto numérico al que pertenezca el exponente:
Cuando el exponente es un número natural, equivale a multiplicar un número por sí mismo varias veces: el exponente determina la cantidad de veces.
Por ejemplo: .
cuando el exponente es un número entero negativo, equivale a la fracción inversa de la base pero con exponente positivo.
cuando el exponente es una fracción irreducible n/m, equivale a una raíz:
Cualquier número elevado a 0 equivale a 1, excepto el caso particular de 00 que, en principio, es una indefinición (ver cero).
La definición de potenciación puede extenderse a exponentes reales, complejos o incluso matriciales
Se escribe an, y se lee: «a elevado a n». Su definición varía según el conjunto numérico al que pertenezca el exponente:
Cuando el exponente es un número natural, equivale a multiplicar un número por sí mismo varias veces: el exponente determina la cantidad de veces.
Por ejemplo: .
cuando el exponente es un número entero negativo, equivale a la fracción inversa de la base pero con exponente positivo.
cuando el exponente es una fracción irreducible n/m, equivale a una raíz:
Cualquier número elevado a 0 equivale a 1, excepto el caso particular de 00 que, en principio, es una indefinición (ver cero).
La definición de potenciación puede extenderse a exponentes reales, complejos o incluso matriciales
Triangulo De Pascal
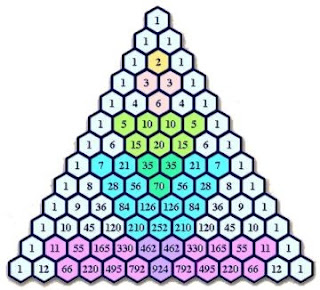
El triángulo de Pascal en matemáticas es un conjunto infinito de números enteros ordenados en forma de triángulo que expresan coeficientes binomiales. El interés del Triángulo de Pascal radica en su aplicación en álgebra y permite calcular de forma sencilla números combinatorios lo que sirve para aplicar el binomio de Newton.
martes, 13 de abril de 2010
Ecuacion Cuadratica
Consideremos la ecuación cuadrática general ax2 + bx + c = 0.
Se puede resolver al completar el cuadrado.
Analizando la raíz cuadrada, se llega a las siguientes conclusiones:
Si b2 es menor que − 4ac los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un numero complejo.
Si b2 es mayor que − 4ac obtendremos dos valores distintos de X reales.
Y si b2 es igual que − 4ac obtendremos dos valores de X reales e iguales.
Al término b2 − 4ac se le llama discriminante.
Se puede resolver al completar el cuadrado.
Analizando la raíz cuadrada, se llega a las siguientes conclusiones:
Si b2 es menor que − 4ac los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un numero complejo.
Si b2 es mayor que − 4ac obtendremos dos valores distintos de X reales.
Y si b2 es igual que − 4ac obtendremos dos valores de X reales e iguales.
Al término b2 − 4ac se le llama discriminante.
Valor Absoluto
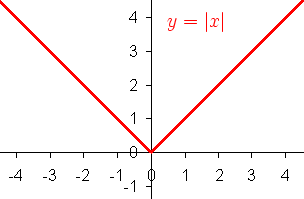
En matemática, el valor absoluto o módulo[1] de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de 3 y de -3.
El valor absoluto está relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.
El valor absoluto está relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.
Inecuaciones Irracionales
Las Palabras Claves Son :
ángulos | aplicaciones económicas | asíntotas | autoevaluación de matemáticas | bibliografía | circunferencia | concavidad | Cónicas | Continuidad | convexidad | coseno | Cramer | Crecimiento | curso cero | decrecimiento | derivada | determinantes | dominio | ecuaciones | ecuaciones irracionales | ecuaciones polinómicas | ecuaciones racionales | ejercicios para resolver | ejercicios resueltos | elipse | enlaces | fracciones | función exponencial | función logarítmica | función potencial | funciones reales | funciones trigonométricas | hipérbola | inecuaciones | inecuaciones irracionales | inecuaciones polinómicas | inecuaciones racionales | Límites | lineales | logaritmos | matemáticas básicas | matemáticas para economistas | matrices | máximo | método de Gauss | mínimo | Números complejos | números decimales | números enteros | números irracionales | números naturales | números racionales | Números reales | operaciones elementales | parábola | pendiente | potencias | puntos | puntos de inflexión | raíces | ramas parabólicas | rango | recta | regla de L´Hôpital | representación gráfica | seno | sistemas | tangente | trigonometría | Vectores
ángulos | aplicaciones económicas | asíntotas | autoevaluación de matemáticas | bibliografía | circunferencia | concavidad | Cónicas | Continuidad | convexidad | coseno | Cramer | Crecimiento | curso cero | decrecimiento | derivada | determinantes | dominio | ecuaciones | ecuaciones irracionales | ecuaciones polinómicas | ecuaciones racionales | ejercicios para resolver | ejercicios resueltos | elipse | enlaces | fracciones | función exponencial | función logarítmica | función potencial | funciones reales | funciones trigonométricas | hipérbola | inecuaciones | inecuaciones irracionales | inecuaciones polinómicas | inecuaciones racionales | Límites | lineales | logaritmos | matemáticas básicas | matemáticas para economistas | matrices | máximo | método de Gauss | mínimo | Números complejos | números decimales | números enteros | números irracionales | números naturales | números racionales | Números reales | operaciones elementales | parábola | pendiente | potencias | puntos | puntos de inflexión | raíces | ramas parabólicas | rango | recta | regla de L´Hôpital | representación gráfica | seno | sistemas | tangente | trigonometría | Vectores
martes, 6 de abril de 2010
INECUACIONES

Una inecuación es una expresión matemática la cual se caracteriza por tener los signos de desigualdad; Siendo una expresión algebraica nos da como resultado un conjunto en el cual la variable independiente puede tomar el valor cualesquiera de ese conjunto cumpliendo esta desigualdad; a este conjunto se le conoce como Intervalo.
Ejemplo
5x+3+2>8+4x
= 5x-4x>8-5
= x>3
Hitoria del calculo

Antiguidade
De acordo com Gauss, Arquimedes, o maior matemático da antigüidade, já apresentava idéias relacionadas ao Cálculo dois séculos antes de Cristo.Na Antiguidade, foram introduzidas algumas idéias do cálculo integral, embora não tenha havido um desenvolvimento dessas idéias de forma rigorosa e sistemática. A função básica do cálculo integral, calcular volumes e áreas, pode ser remontada ao Papiro Egípcio de Moscow (1800 a.C.), no qual um egípcio trabalhou o volume de um frustum piramidal. Eudoxus (408-355 a.C.) usou o método da exaustão para calcular áreas e volumes. Arquimedes (287-212 a.C.) levou essa idéia além, inventando a heurística, que se aproxima do cálculo integral. O método da exaustão foi redescoberto na China por Liu Hui no século III, que o usou para encontrar a área do círculo. O método também foi usado por Zu Chongzhi século V, para achar o volume de uma esfera.
Idade Média
Na Idade Média, o matemático indiano Aryabhata usou a noção infinitesimal em 499 d.C. expressando-a em um problema de astronomia na forma de uma equação diferencial básica. Essa equação levou Bhāskara II no século XII a desenvolver uma derivada prematura representado uma mudança infinitesimal, e ele desenvolveu também o que seria uma forma primitiva do "Teorema de Rolle".
No século XII, o matemático persa Sharaf al-Din al-Tusi descobriu a derivada de polinômios cúbicos, um resultado importante no cálculo diferencial. No século XIV, Madhava de Sangamagrama, juntamente com outros matemáticos-astrônomos da Escola Kerala de Astronomia e Matemática, descreveu casos especiais da Série de Taylor, que no texto são tratadas como Yuktibhasa.
Idade Moderna
Sir Isaac Newton aplicou o cálculo às suas leis do movimento e a outros conceitos matemáticos-físicos.No Idade Moderna, descobertas independentes no cálculo foram feitas no início do século XVII no Japão por matemáticos como Seki Kowa, que expandiu o método de exaustão. Na Europa, a segunda metade do século XVII foi uma época de grandes inovações. O Cálculo abriu novas oportunidades na física-matemática de resolver problemas muito antigos que até então não haviam sido solucionados. Muitos matemáticos contribuíram para essas descobertas, notavelmente John Wallis e Isaac Barrow. James Gregory proveu um caso especial do segundo teorema fundamental do cálculo em 1668.
Coube a Gottfried Wilhelm von Leibniz e a Isaac Newton recolher essas idéias e juntá-las em um corpo teórico que viria a constituir o cálculo. A ambos é atribuída a simultânea e independente invenção do cálculo. Leibnitz foi originalmente acusado de plagiar os trabalhos não publicados de Isaac Newton; hoje porém é considerado o inventor do cálculo, juntamente com Newton. Historicamente Newton foi o primeiro a aplicar o cálculo à física ao passo que Leibniz desenvolveu a notação utilizada até os dias de hoje. O argumento histórico para conferir aos dois a invenção do cálculo é que ambos chegaram de maneiras distintas ao teorema fundamental do cálculo.
Gottfried Wilhelm Leibniz: o inventor do cálculo, juntamente com Newton.Quando Newton e Leibniz publicaram seus resultados, houve uma grande controvérsia de qual matemático (e portanto que país: Inglaterra ou Alemanha) merecia o crédito. Newton derivou seus resultados primeiro, mas Leibniz publicou primeiro. Newton argumentou que Leibniz roubou idéias de seus escritos não publicados, que Newton à época compartilhara com alguns poucos membros da Sociedade Real. Esta controvérsia dividiu os matemáticos ingleses dos matemáticos alemães por muitos anos. Um exame cuidadoso dos escritos de Leibniz e Newton mostra que ambos chegaram a seus resultados independentemente, com Leibniz iniciando com integração e Newton com diferenciação. Nos dias de hoje tem-se que Newton e Leibniz descobriram o cálculo independentemente. Leibniz, porém, foi quem deu o nome cálculo à nova disciplina, Newton a chamara de "A ciência dos fluxos".
Desde o tempo de Leibniz e Newton, muitos matemáticos contribuíram
introduccion al calculo

Las matemáticas o la matemática (del lat. mathematĭca, y éste del gr. μαθηματικά, derivado de μάθημα, conocimiento) es una ciencia que, a partir de notaciones básicas exactas y a través del razonamiento lógico, estudia las propiedades y relaciones cuantitativas entre los entes abstractos (números, figuras geométricas, símbolos).[2] Mediante las matemáticas conocemos las cantidades, las estructuras, el espacio y los cambios. Los matemáticos buscan patrones,[3] [4] formulan nuevas conjeturas e intentan alcanzar la verdad matemática mediante rigurosas deducciones. Éstas les permiten establecer los axiomas y las definiciones apropiados para dicho fin.
Suscribirse a:
Comentarios (Atom)
